Διαφορά μεταξύ ελλειψοειδούς και ωοειδούς: ελλειπτική με οβάλ
Ελλειψη και οβάλ
παρόμοια γεωμετρικά σχήματα. Ως εκ τούτου, οι κατάλληλες έννοιες τους προκαλούν μερικές φορές σύγχυση. Και οι δύο είναι επίπεδες μορφές με παρόμοια εμφάνιση, όπως η επιμήκης φύση και οι ομαλές καμπύλες τους καθιστούν σχεδόν ταυτόσημες. Ωστόσο, είναι διαφορετικές και οι λεπτές διαφορές τους συζητούνται σε αυτό το άρθρο.
Έλλειψη
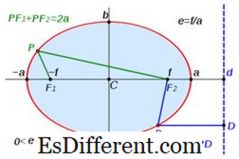
Όταν η τομή της κωνικής επιφάνειας και της επίπεδης επιφάνειας παράγει μια κλειστή καμπύλη, είναι γνωστή ως έλλειψη. Έχει εκκεντρότητα μεταξύ μηδέν και ενός (0 Το τμήμα γραμμής που διέρχεται από τις εστίες είναι γνωστό ως ο κύριος άξονας και ο άξονας κάθετος προς τον κύριο άξονα και που διέρχεται από το κέντρο Η διάμετρος κατά μήκος αυτών των αξόνων είναι γνωστή ως η εγκάρσια διάμετρος και η διάμετρος του συζυγούς αντίστοιχα.Ο μισός από τους κύριους άξονες είναι γνωστός ως ημι-κύριος άξονας και ο μισός από τους δευτερεύοντες άξονες είναι γνωστός ως κάθε σημείο F1 και F2 είναι γνωστά ως εστίες ελλειψίας και μήκη PF + PF 2 < = 2a, όπου P είναι ένα αυθαίρετο σημείο στην έλλειψη. Η εκκεντρότητα e ορίζεται ως ο λόγος μεταξύ της απόστασης από την εστίαση στο αυθαίρετο σημείο (PF 2 ) και της κάθετης απόστασης από την αυθαίρετη από το directrix (PD) και ισούται με την απόσταση μεταξύ των δύο πυρήνων και του ημικυκλικού άξονα: e = PF / PD = f / a Όταν ο ημι-κύριος άξονας και ο ημι-δευτερεύων άξονας συμπίπτει με των καρτεσιανών αξόνων, η γενική εξίσωση της ελλείψεως δίδεται ως εξής. x 2 / a 2 + y 2 εφαρμογές, ειδικά στη φυσική. Οι τροχιές των πλανητών στο ηλιακό σύστημα είναι ελλειπτικές με τον ήλιο ως μία εστίαση. Οι ανακλαστήρες για κεραίες και ακουστικές συσκευές κατασκευάζονται σε ελλειπτική μορφή για να επωφεληθούν από το γεγονός ότι οποιαδήποτε εκπομπή σχηματίζει μια εστίαση θα συγκλίνει στην άλλη εστίαση. Οβάλ Το ωοειδές δεν είναι ένα ακριβές σχήμα στα μαθηματικά. Αλλά αναγνωρίζεται ως σχήμα όταν ένας κύκλος τεντώνεται σε δύο απέναντι άκρα, δηλ. μι. παρόμοια με τις ελλείψεις ή παρόμοια με το σχήμα ενός αυγού. Ωστόσο, οι οβάλ δεν είναι πάντα ελλείψεις. Οι οβάλ έχουν τις ακόλουθες ιδιότητες, οι οποίες τις διαφοροποιούν από άλλες καμπύλες μορφές. • Απλές, ομαλές, κυρτές κλειστές καμπύλες επιπέδου. (Η εξίσωση του ωοειδούς είναι διαφοροποιήσιμη σε όλα τα σημεία) • Μοιράζονται περίπου την ίδια εικόνα με τις ελλείψεις. • Τουλάχιστον υπάρχει ένας άξονας συμμετρίας. Τα ωοειδή Cassini, οι ελλειπτικές καμπύλες, η υπερ ελλειψία και το καρτεσιανό ωοειδές είναι ωοειδή σχήματα που βρίσκονται στα μαθηματικά. Ποια είναι η διαφορά μεταξύ του ελλειπτικού και του οβάλ; • Οι ελλείψεις είναι κωνικές τομές με εκκεντρότητα (ε) μεταξύ 0 και 1, ενώ οι οβάλ δεν είναι ακριβείς γεωμετρικοί αριθμοί στα μαθηματικά. • Μια ελλειπτική είναι πάντα ωοειδής, αλλά ένα ωοειδές δεν είναι πάντα ελλειπτική. (Οι ελλείψεις είναι ένα υποσύνολο των ωοειδών) • Η ελλειπτική έχει δύο συμμετρικούς άξονες (ημίξηρα και ημίξηρα), αλλά οι οβάλ μπορεί να έχουν είτε έναν είτε δύο συμμετρικό άξονα.