Διαφορά μεταξύ ορθογώνιου και ρομβοειδούς: ορθογώνιο Vs ορθογώνιο

Ορθογώνιο και Rhombus

Η γεωμετρία αυτών των μορφών ήταν γνωστή στον άνθρωπο για χιλιάδες χρόνια. Το θέμα εξετάζεται ρητά στο βιβλίο "Στοιχεία" που γράφει ο Έλληνας μαθηματικός Euclid.

Παράλληλο γραφή

Το παράλληλο γραμματισμό μπορεί να οριστεί ως η γεωμετρική μορφή με τέσσερις πλευρές, με αντίθετες πλευρές παράλληλες μεταξύ τους. Πιο συγκεκριμένα είναι ένα τετράπλευρο με δύο ζεύγη παράλληλων πλευρών. Αυτή η παράλληλη φύση δίνει πολλά γεωμετρικά χαρακτηριστικά στα παράλληλα γραφήματα.

Ένα τετράπλευρο είναι ένα παραλληλόγραμμο εάν εντοπιστούν τα ακόλουθα γεωμετρικά χαρακτηριστικά.

• Δύο ζεύγη αντίθετων πλευρών έχουν ίσο μήκος. (AB = DC, AD = BC)

• Δύο ζεύγη αντιτιθέμενων γωνιών είναι ίσου μεγέθους. (

)

• Εάν οι γειτονικές γωνίες είναι συμπληρωματικές

• Ένα ζεύγος πλευρών, οι οποίες αντιτίθενται μεταξύ τους, είναι παράλληλες και ίσες σε μήκος. (ΑΒ = DC & ΑΒ διόδουDC)

• Οι διαγώνιοι διασταυρώνονται μεταξύ τους (AO = OC, BO = OD)

• Κάθε διαγώνιος διαιρεί το τετράπλευρο σε δύο όμοια τρίγωνα. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Επιπλέον, το άθροισμα των τετραγώνων των πλευρών είναι ίσο με το άθροισμα των τετραγώνων των διαγωνίων. Αυτό μερικές φορές αναφέρεται ως ο νόμος παραλληλογράμμου και έχει εκτεταμένες εφαρμογές στη φυσική και στη μηχανική. (² + ² + CD ² 2 ⁾ Καθένα από τα παραπάνω χαρακτηριστικά μπορεί να χρησιμοποιηθεί ως ιδιότητες, αφού διαπιστωθεί ότι το τετράπλευρο είναι ένα παραλληλόγραμμο. ^{Η περιοχή του παραλληλογράμμου μπορεί να υπολογιστεί από το προϊόν του μήκους μιας πλευράς και του ύψους στην αντίθετη πλευρά. Ως εκ τούτου, η περιοχή του παραλληλογράμμου μπορεί να αναφέρεται ως} Περιοχή παραλληλόγραμμου = βάση × ύψος = ^AB ×

h

Η περιοχή του παραλληλογράμμου είναι ανεξάρτητη από το σχήμα του μεμονωμένου παραλληλογράμμου. Εξαρτάται μόνο από το μήκος βάσης και το κάθετο ύψος.

Εάν οι πλευρές ενός παραλληλογράμμου μπορούν να αναπαρασταθούν από δύο φορείς, η περιοχή μπορεί να ληφθεί από το μέγεθος του διανυσματικού προϊόντος (εγκάρσιο προϊόν) των δύο γειτονικών διανυσμάτων. Αν οι πλευρές AB και AD αντιπροσωπεύονται από τους φορείς () και () αντίστοιχα, η περιοχή του παραλληλογράμμου δίνεται από το

, όπου α είναι η γωνία

>.

Ακολουθούν μερικές προηγμένες ιδιότητες του παραλληλογράμμου.

• Η περιοχή ενός παραλληλογράμμου είναι διπλάσια από την περιοχή ενός τριγώνου που δημιουργείται από οποιαδήποτε από τις διαγώνιες του.

• Η περιοχή του παραλληλογράμμου διαιρείται στο μισό από κάθε γραμμή που διέρχεται από το μέσο σημείο.

• Κάθε μη-εκφυλισμένος συγγενικός μετασχηματισμός παίρνει ένα παράλληλο διάγραμμα σε ένα άλλο παραλληλόγραμμο

• Ένα παραλληλόγραμμο έχει περιστροφική συμμετρία της σειράς 2

• Το άθροισμα των αποστάσεων από οποιοδήποτε εσωτερικό σημείο ενός παραλληλογράμμου στις πλευρές είναι ανεξάρτητο από η θέση του σημείου

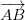
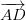
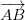
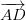
Ορθογώνιο

Ένα τετράπλευρο με τέσσερις ορθές γωνίες είναι γνωστό ως ορθογώνιο. Είναι μια ειδική περίπτωση του παραλληλογράμμου όπου οι γωνίες μεταξύ οποιωνδήποτε δύο γειτονικών πλευρών είναι ορθές γωνίες.

Εκτός από όλες τις ιδιότητες ενός παραλληλογράμμου, μπορούν να αναγνωριστούν πρόσθετα χαρακτηριστικά κατά την εξέταση της γεωμετρίας του ορθογωνίου.

• Κάθε γωνία στις κορυφές είναι ορθή γωνία.

• Οι διαγώνιοι είναι ίσοι σε μήκος, και διασταυρώνονται μεταξύ τους. Επομένως, τα διαχωρισμένα τμήματα είναι επίσης ίσα σε μήκος.

• Το μήκος των διαγωνίων μπορεί να υπολογιστεί χρησιμοποιώντας το θεώρημα του Pythagoras:

PQ

2

+ PS

2

μειώνει στο προϊόν το μήκος και το πλάτος.

Περιοχή ορθογωνίου = μήκος × πλάτος

• Πολλές συμμετρικές ιδιότητες βρίσκονται σε ένα ορθογώνιο, όπως π.χ. ^{- Ένα ορθογώνιο είναι κυκλικό, όπου όλες οι κορυφές μπορούν να τοποθετηθούν στην περίμετρο ενός κύκλου.} - Είναι ισόπλευρο, όπου όλες οι γωνίες είναι ίσες. ^{- Είναι ισογωνική, όπου όλες οι γωνίες βρίσκονται μέσα στην ίδια τροχιά συμμετρίας.} - Έχει τόσο ανακλαστική συμμετρία όσο και περιστροφική συμμετρία. ^Rhombus

Ένα τετράπλευρο με όλες τις πλευρές ίσες σε μήκος είναι γνωστό ως ρόμβος. Ονομάζεται επίσης ως

ισόπλευρο τετράπλευρο

. Θεωρείται ότι έχει σχήμα διαμαντιού, παρόμοιο με αυτό των καρτών παιχνιδιού.

Το Rhombus είναι επίσης μια ειδική περίπτωση του παραλληλογράμμου. Μπορεί να θεωρηθεί παράλληλο με όλες τις τέσσερις πλευρές ίσες. Και έχει τις παρακάτω ειδικές ιδιότητες, εκτός από τις ιδιότητες ενός παραλληλογράμμου.

• Οι διαγώνιοι του ρόμβου κάθεται μεταξύ τους σε ορθή γωνία. οι διαγώνιοι είναι κάθετοι.

• Οι διαγώνιοι διευρύνουν τις δύο αντίθετες εσωτερικές γωνίες.

• Τουλάχιστον δύο από τις παρακείμενες πλευρές έχουν ίσο μήκος.

Η περιοχή του ρόμβου μπορεί να υπολογιστεί με την ίδια μέθοδο με το παραλληλόγραμμο.

Ποια είναι η διαφορά μεταξύ του Rhombus και του Rectangle; • Ο λοβός και το ορθογώνιο είναι τετράπλευρα. Το ορθογώνιο και το ρομβο είναι ειδικές περιπτώσεις των παραλληλογράμμων. • Η περιοχή μπορεί να υπολογιστεί χρησιμοποιώντας τη βάση

βάση × ύψος

.

• Λαμβάνοντας υπόψη τις διαγωνίες.

- Οι διαγώνιοι του ρόμβου κάθεται μεταξύ τους σε ορθή γωνία και τα τρίγωνα που σχηματίζονται είναι ισόπλευρα.

- Οι διαγώνιοι του ορθογωνίου είναι ίσοι σε μήκος και διχοτομούν ο ένας τον άλλον. τα διαχωρισμένα τμήματα είναι ίσα σε μήκος. Οι διαγωνίσεις διχοτομούν το ορθογώνιο σε δύο όμοια ορθά τρίγωνα.

• Λαμβάνοντας υπόψη τις εσωτερικές γωνίες.

- Οι εσωτερικές γωνίες του ρόμβου διαχωρίζονται από τις διαγώνιες

- Και οι τέσσερις εσωτερικές γωνίες του ορθογωνίου είναι ορθές γωνίες. • Λαμβάνοντας υπόψη τις πλευρές. - Καθώς και οι τέσσερις πλευρές είναι ίσες σε ένα ρομβοειδές, τέσσερις φορές το τετράγωνο μιας πλευράς είναι ίσο με το άθροισμα των τετραγώνων της διαγώνιας (χρησιμοποιώντας τον νόμο των παραλληλογράμων)

- Στα ορθογώνια, το άθροισμα των τετραγώνων των δύο γειτονικών πλευρών είναι ίση με το τετράγωνο της διαγώνιο στις άκρες.(Κανόνας του Πυθαγόρα)