Διαφορά μεταξύ της επαγωγής και της αφαίρεσης: επαγωγή έναντι αφαίρεσης
Εισαγωγή έναντι Αφαίρεσης
Στη λογική θεωρία, η επαγωγή και η αφαίρεση είναι προεξέχουσες μέθοδοι συλλογισμού. Μερικές φορές οι άνθρωποι χρησιμοποιούν επαγωγή ως υποκατάστατο της έκπτωσης και εσφαλμένα κάνουν ψευδείς και ανακριβείς δηλώσεις.
Αφαίρεση
Η μέθοδος απόσβεσης χρησιμοποιεί πιο γενικές πληροφορίες για να καταλήξει σε ένα συγκεκριμένο συμπέρασμα. Μπορεί να θεωρηθεί ως λογική όπου το συμπέρασμα θεωρείται ως το λογικό επακόλουθο της παραδοχής ή του επιχειρήματος. Η εγκυρότητα του συμπεράσματος βασίζεται στην εγκυρότητα της υπόθεσης ή του επιχειρήματος. Το συμπέρασμα εξαρτάται έντονα από τις εγκαταστάσεις ή τα επιχειρήματα σε μια μέθοδο αφαίρεσης.
Ακολουθούν μερικά παραδείγματα λογικής αφαίρεσης.
o Το ηλιακό σύστημα έχει 8 πλανήτες
o Η Γη είναι ένας πλανήτης στο ηλιακό σύστημα
o Επομένως, η Γη είναι ένας από τους οκτώ πλανήτες.
Λαμβάνοντας υπόψη ένα άλλο παράδειγμα
o Το κόμμα Α κέρδισε τις εκλογές
o Ο κ. Χ ήταν ο υποψήφιος από το κόμμα Α
o Επομένως, ο κ. Χ θα πάρει το αξίωμα.
Σε μια άλλη εικόνα, μπορεί να θεωρηθεί ως μια ροή από ένα ευρύτερο γενικό σύνολο πληροφοριών σε ένα στενό αλλά συγκεκριμένο σύνολο πληροφοριών. Η διαδικασία αφαίρεσης μπορεί να συνοψιστεί στα ακόλουθα στάδια.
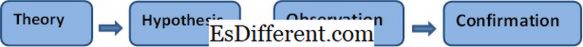
Επαγωγή
Η επαγωγή είναι μια διαδικασία όπου τα μεμονωμένα επιχειρήματα και οι χώροι χρησιμοποιούνται για να αναπτύξουν μια γενίκευση ή ένα συμπέρασμα που μπορεί να αποδοθεί σε πολύ περισσότερα από τα αρχικά θέματα. Στη μέθοδο αυτή, το συμπέρασμα μπορεί να επικυρωθεί ή να διαψευσθεί από τις προηγούμενες εγκαταστάσεις.
Ακολουθούν ορισμένα παραδείγματα για επαγωγική συλλογιστική.
o Όλα τα ποτάμια που διασχίστηκα ρέουν προς τον ωκεανό. Επομένως, όλοι οι ποταμοί ρέουν προς τον ωκεανό.
Η παραπάνω επαγωγή ισχύει για όλα τα ποτάμια. Εξετάστε μια άλλη επαγωγή
o Μήνας του Αυγούστου έζησε ξηρασία για τα τελευταία δέκα χρόνια. Συνεπώς, θα υπάρξουν συνθήκες ξηρασίας εδώ για κάθε Αύγουστο στο μέλλον. Αυτή η επαγωγή μπορεί να ισχύει ή και όχι.
Η διαδικασία εισαγωγής μπορεί να θεωρηθεί ότι φτάνει σε ένα γενικό συμπέρασμα για ένα μεγαλύτερο σύνολο εξετάζοντας τα αποτελέσματα μερικών πολύ συγκεκριμένων περιπτώσεων. Η διαδικασία μπορεί να θεωρηθεί ως εξής:

Εισαγωγή έναντι αφαίρεσης
• Η αφαίρεση είναι μια μορφή λογικής που επιτυγχάνει ένα συγκεκριμένο συμπέρασμα από το γενικό, αντλώντας τα απαραίτητα συμπεράσματα από τις εγκαταστάσεις. (Στην έκπτωση, η μεγαλύτερη κατανόηση χρησιμοποιείται για να καταλήξει σε συμπέρασμα για κάτι παρόμοιο, αλλά μικρότερο.)
• Η επαγωγή είναι μια μορφή λογικής που επιτυγχάνει γενικό αποτέλεσμα από τις συγκεκριμένες περιπτώσεις, αντλώντας πιθανά συμπεράσματα από οι εγκαταστάσεις.(Κατά την επαγωγή, δημιουργείται μια μεγαλύτερη εικόνα χρησιμοποιώντας μερικές συγκεκριμένες διαθέσιμες παρατηρήσεις.)



