Διαφορά μεταξύ οριστικών και αόριστων ενοτήτων Η διαφορά μεταξύ του
Ο υπολογισμός είναι ένας σημαντικός κλάδος των μαθηματικών και η διαφοροποίηση παίζει έναν κρίσιμο ρόλο στον υπολογισμό. Η αντίστροφη διαδικασία της διαφοροποίησης είναι γνωστή ως ολοκλήρωση, και το αντίστροφο είναι γνωστό ως το ενιαίο, ή απλά θέτει, το αντίστροφο της διαφοροποίησης δίνει ένα ενιαίο. Με βάση τα αποτελέσματα που παράγουν τα ολοκληρώματα χωρίζονται σε δύο κατηγορίες, δηλαδή., οριστικά και αόριστα ολοκληρώματα.
Ολοκληρωμένο
->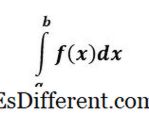
Το οριστικό ολοκλήρωμα του f (x) είναι NUMBER και αντιπροσωπεύει την περιοχή κάτω από την καμπύλη f (x) έως x = b . Ένα οριστικό ολοκλήρωμα έχει ανώτερα και κατώτερα όρια στα ολοκληρώματα και ονομάζεται ορισμός επειδή, στο τέλος του προβλήματος, έχουμε έναν αριθμό - είναι μια οριστική απάντηση.
Η απεριόριστη ολοκλήρωση του f (x) είναι μια ΛΕΙΤΟΥΡΓΙΑ και απαντά στην ερώτηση, "Ποια λειτουργία όταν διαφοροποιείται δίνει
f (x); "

Με αόριστο ολοκληρωμένο δεν υπάρχουν ανώτερα και κατώτερα όρια για το ολοκλήρωμα εδώ και αυτό που θα πάρουμε είναι μια απάντηση που έχει ακόμα το x σε αυτό και θα έχει επίσης σταθερή (συνήθως σημειωμένο με
C ).
F
οδηγεί σε μια άλλη συνάρτηση
f , και η ολοκλήρωση του f δίνει το ολοκλήρωμα. Συμβολικά, αυτό είναι γραμμένο ως F (x) = ∫ƒ (x) dx ή F = ∫ƒ dx
είναι λειτουργίες
x
, και
F είναι διαφοροποιήσιμες. Στην παραπάνω μορφή, ονομάζεται αναπόσπαστο τμήμα του Reimann και η προκύπτουσα συνάρτηση συνοδεύει μια αυθαίρετη σταθερά. Ένα αόριστο ολοκλήρωμα παράγει συχνά μια οικογένεια λειτουργιών. Επομένως, το ολοκλήρωμα είναι αόριστο. Η ολοκλήρωση και η διαδικασία ολοκλήρωσης βρίσκονται στο επίκεντρο της επίλυσης των διαφορικών εξισώσεων. Ωστόσο, σε αντίθεση με τα βήματα στη διαφοροποίηση, τα βήματα στην ολοκλήρωση δεν ακολουθούν πάντοτε μια σαφή και τυποποιημένη ρουτίνα. Περιστασιακά, βλέπουμε ότι η λύση δεν μπορεί να εκφραστεί ρητά από την άποψη της στοιχειώδους λειτουργίας. Στην περίπτωση αυτή, η αναλυτική λύση συχνά δίνεται με τη μορφή αόριστου ενιαίου. Το Θεμελιώδες Θεώρημα του Λογισμού Το οριστικό και το αόριστο ολοκλήρωμα συνδέονται με το Θεμελιώδες Θεώρημα του Λογισμού ως εξής: Για να υπολογίσετε ένα ορισμένο ακέραιο , βρείτε το απεριόριστο ολοκλήρωμα > (γνωστό και ως αντι-παράγωγο) της συνάρτησης και να αξιολογηθεί στα τελικά σημεία x = a
και
x = b
Η διαφορά μεταξύ οριστικών και απεριόριστων ολοκληρώσεων θα είναι εμφανής μόλις αξιολογήσουμε τα ολοκληρώματα για την ίδια λειτουργία. Εξετάστε το ακόλουθο ολοκλήρωμα: Εντάξει. Ας κάνουμε και τα δύο και βλέπουμε τη διαφορά. Για την ολοκλήρωση, πρέπει να προσθέσουμε μία στο ευρετήριο που μας οδηγεί στην ακόλουθη έκφραση: Σε αυτό το χρονικό σημείο C είναι απλώς μια σταθερά για εμάς. Απαιτούνται πρόσθετες πληροφορίες στο πρόβλημα για να προσδιοριστεί η ακριβής τιμή C .
Ας αξιολογήσουμε το ίδιο σύμπλεγμα στην οριστική του μορφή i. μι., με τα ανώτερα και κατώτερα όρια που περιλαμβάνονται.
Από γραφική παράσταση, υπολογίζουμε τώρα την περιοχή κάτω από την καμπύλη

f (x) = y
3
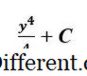
μεταξύ y = 2 και y = 3 >. Το πρώτο βήμα αυτής της αξιολόγησης είναι το ίδιο με την απεριόριστη ολοκληρωμένη αξιολόγηση. Η μόνη διαφορά είναι ότι αυτή τη φορά δεν προσθέτουμε το σταθερό
C

. Η έκφραση σε αυτή την περίπτωση φαίνεται ως εξής: Αυτή είναι η σειρά οδηγεί σε: Ουσιαστικά, αντικαταστήσαμε 3 και στη συνέχεια 2 στην έκφραση και αποκτήσαμε τη διαφορά μεταξύ τους. Αυτή είναι η οριστική τιμή σε αντίθεση με τη χρήση σταθερών C νωρίτερα. Ας εξερευνήσουμε τον σταθερό παράγοντα (σε σχέση με το αόριστο ολοκλήρωμα) με περισσότερες λεπτομέρειες.
Εάν η διαφορά y 3
είναι

3y

2, τότε ∫ 3y
2
dy = y 3 3 3 2 μπορεί να είναι η διαφορά πολλών εκφράσεων, μεταξύ των οποίων
> y 3 +7 , κτλ … Αυτό σημαίνει ότι η αντιστροφή δεν είναι μοναδική δεδομένου ότι η σταθερά δεν καταγράφεται κατά τη διάρκεια της λειτουργίας. Έτσι, γενικά,
3y 2 είναι η διαφορά y 3 + C όπου C είναι σταθερή. Παρεμπιπτόντως, το C είναι γνωστό ως 'σταθερά ολοκλήρωσης' . Γράφουμε το εξής:
∫ 3y 2 . dx = γ 3 + C Οι τεχνικές ενσωμάτωσης για ένα αόριστο ολοκλήρωμα, όπως η αναζήτηση πίνακα ή η ενσωμάτωση Risch, μπορούν να προσθέσουν νέες ασυνέχειες κατά τη διαδικασία ολοκλήρωσης. Αυτές οι νέες ασυνέχειες εμφανίζονται επειδή τα αντι-παράγωγα μπορούν να απαιτήσουν την εισαγωγή πολύπλοκων λογαρίθμων. Οι σύνθετοι λογάριθμοι έχουν μια ασυνέχεια άλματος όταν το όρισμα διασχίζει τον αρνητικό πραγματικό άξονα και οι αλγόριθμοι ολοκλήρωσης μερικές φορές δεν μπορούν να βρουν μια αναπαράσταση όπου αυτά τα άλματα ακυρώνονται. Αν το οριστικό ολοκλήρωμα αξιολογείται πρώτα από τον υπολογισμό ενός απεριόριστου ενιαίου και στη συνέχεια την υποκατάσταση των ορίων ολοκλήρωσης στο αποτέλεσμα, πρέπει να γνωρίζουμε ότι η αόριστη ενσωμάτωση μπορεί να προκαλέσει ασυνέχειες. Εάν συμβαίνει, επιπλέον, πρέπει να διερευνήσουμε τις ασυνέχειες στο διάστημα ολοκλήρωσης.



