Διαφορά μεταξύ Centroid Circumcenter Incenter και Orthocenter | Centroid vs Circumcenter vs Incenter εναντίον Orthocenter

περίκεντρο, incenter, Ορθόκεντρο vs Κέντρο βάρους

Circumcenter: circumcenter είναι το σημείο τομής τριών κάθετων διχοτόμων ενός τριγώνου . Το Circumcenter είναι το κέντρο του circumcircle , ο οποίος είναι ένας κύκλος που διέρχεται και από τις τρεις κορυφές ενός τριγώνου.

Για να σχεδιάσετε το circumcenter δημιουργήστε δύο κάθετες διχοτόμους στις πλευρές του τριγώνου. Το σημείο τομής δίνει το circumcenter. Μια διχοτόμηση μπορεί να δημιουργηθεί χρησιμοποιώντας την πυξίδα και την ευθεία άκρη του χάρακα. Ρυθμίστε την πυξίδα σε ακτίνα, η οποία είναι μεγαλύτερη από το ήμισυ του μήκους του τμήματος γραμμής. Στη συνέχεια, κάντε δύο τόξα σε κάθε πλευρά του τμήματος με ένα άκρο ως το κέντρο του τόξου. Επαναλάβετε τη διαδικασία με το άλλο άκρο του τμήματος. Τα τέσσερα τόξα δημιουργούν δύο σημεία τομής σε κάθε πλευρά του τμήματος. Σχεδιάστε μια γραμμή που ενώνει αυτά τα δύο σημεία με τη βοήθεια του χάρακα, και αυτό θα δώσει την κάθετη διχοτόμηση του τμήματος.

Για να δημιουργήσετε τον circumcircle, σχεδιάστε έναν κύκλο με το circumcenter ως το κέντρο και το μήκος μεταξύ circumcenter και μια κορυφή ως την ακτίνα του κύκλου.

Incenter: Incenter είναι το σημείο τομής των τριών γωνιακών bisector s. Incenter είναι το κέντρο του κύκλου με περιφέρεια που τέμνει τις τρεις πλευρές του τριγώνου.

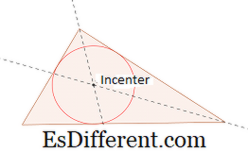
Για να σχεδιάσετε το κίνητρο ενός τριγώνου, δημιουργήστε δύο εσωτερικές γωνίες του τριγώνου . Το σημείο τομής των δύο γωνιακών διχοτόμων δίνει το κίνητρο. Για να σχεδιάσετε τη γωνία διχοτόμησης, κάντε δύο τόξα σε κάθε ένα από τα χέρια με την ίδια ακτίνα. Αυτό παρέχει δύο σημεία (ένα για κάθε βραχίονα) στους βραχίονες της γωνίας. Στη συνέχεια, λαμβάνοντας κάθε σημείο στους βραχίονες ως τα κέντρα, σχεδιάστε δύο ακόμη τόξα. Το σημείο που κατασκευάζεται από τη διασταύρωση αυτών των δύο τόξων δίνει ένα τρίτο σημείο. Μια γραμμή που ενώνει την κορυφή της γωνίας και το τρίτο σημείο δίνει τη διχοτόμηση γωνίας.

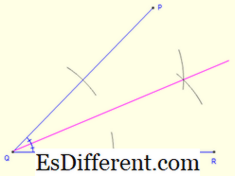
Για να δημιουργήσετε το incircle , κατασκευάστε ένα τμήμα γραμμής κάθετο προς οποιαδήποτε πλευρά, η οποία διέρχεται από το κίνητρο. Λαμβάνοντας το μήκος μεταξύ της βάσης της κάθετης και της κινήτριας ως της ακτίνας, σχεδιάστε έναν πλήρη κύκλο.

Orthocenter: Το Orthocenter είναι το σημείο τομής των τριών υψών (υψομέτρων) του τριγώνου.

Για να δημιουργήσετε το orthocenter, σχεδιάστε δύο υψόμετρα ενός τριγώνου . Ένα τμήμα γραμμής κάθετο προς μία πλευρά που διέρχεται από την αντίθετη κορυφή ονομάζεται ύψος.Για να σχεδιάσετε μια κάθετη γραμμή που διέρχεται από ένα σημείο, σημειώστε πρώτα δύο τόξα στη γραμμή με το σημείο ως το κέντρο. Στη συνέχεια, δημιουργήστε άλλα δύο τόξα με καθένα από τα σημεία διασταύρωσης ως κέντρο. Σχεδιάστε ένα τμήμα γραμμής που ενώνει το πρώτο σημείο και το τελικά κατασκευασμένο σημείο και αυτό δίνει τη γραμμή κάθετη στο τμήμα γραμμής και διέρχεται από το πρώτο σημείο. Το σημείο τομής των δύο υψών δίνει το orthocenter.

Centroid: Το Centroid είναι το σημείο τομής των τριών μέσων ενός τριγώνου . Το κεντροειδές διαιρεί κάθε διάμεσο σε αναλογία 1: 2 και το κέντρο της μάζας ενός ομοιόμορφου τριγωνικού στρώματος βρίσκεται σε αυτό το σημείο.

Για να καθορίσετε το κέντρο, δημιουργήστε δύο διαμέτρους του τριγώνου. Για τη δημιουργία ενός μέσου, σημειώστε το μέσο της πλευράς. Στη συνέχεια, κατασκευάστε ένα τμήμα γραμμής που ενώνει το μέσο και την αντίθετη κορυφή του τριγώνου. Το σημείο τομής των μεσαίων δίνει το κεντρομόνιο ενός τριγώνου.

Ποιες είναι οι διαφορές μεταξύ των Circumcenter, Incenter, Orthocenter και Centroid;

• Το Circumcenter δημιουργείται με τη χρήση των κάθετων διχοτόμων του τριγώνου.

• Οι δημιουργοί δημιουργούνται με τη χρήση των γωνιών των τριγώνων.

• Το Orthocenter δημιουργείται χρησιμοποιώντας τα ύψη (υψόμετρα) του τριγώνου.

• Το Centroid δημιουργείται χρησιμοποιώντας τους διαμέσου του τριγώνου.

• Και το circumcenter και το incenter έχουν συσχετισμένους κύκλους με συγκεκριμένες γεωμετρικές ιδιότητες.

• Το Centroid είναι το γεωμετρικό κέντρο του τριγώνου , το οποίο είναι το κέντρο της μάζας ενός ομοιόμορφου τριγωνικού ελάσματος.

• Για ένα μη ισόπλευρο τρίγωνο, το circumcenter, το orthocenter και το centroid βρίσκονται σε ευθεία γραμμή και η γραμμή είναι γνωστή ως γραμμή Euler .