Διαφορά μεταξύ ολοκλήρωσης και αθροίσματος: ολοκλήρωση Vs αθροιστική σύγκριση

Summation

Στα παραπάνω μαθηματικά γυμνασίου, η ολοκλήρωση και η αθροιστική συσχέτιση απαντώνται συχνά στις μαθηματικές επεμβάσεις. Χρησιμοποιούνται φαινομενικά ως διαφορετικά εργαλεία και σε διαφορετικές καταστάσεις, αλλά μοιράζονται μια πολύ στενή σχέση.

Περισσότερες πληροφορίες για την Summation

Summation είναι η λειτουργία της προσθήκης μιας ακολουθίας αριθμών και η λειτουργία συχνά υποδηλώνεται από την ελληνική επιστολή του κεφαλαίου sigma Σ. Χρησιμοποιείται για να συντομεύει την άθροιση και είναι ίσο με το άθροισμα / σύνολο της ακολουθίας. Συχνά χρησιμοποιούνται για να αντιπροσωπεύσουν τη σειρά, η οποία ουσιαστικά είναι άπειρες ακολουθίες που συνοψίζονται. Μπορούν επίσης να χρησιμοποιηθούν για να υποδείξουν το άθροισμα των διανυσμάτων, μητρών ή πολυωνύμων.

Η άθροιση γίνεται συνήθως για ένα εύρος τιμών που μπορεί να αναπαρασταθεί από έναν γενικό όρο, όπως μια σειρά που έχει έναν κοινό όρο. Το σημείο εκκίνησης και το τελικό σημείο του αθροίσματος είναι γνωστά ως το κάτω και ανώτερο όριο του αθροίσματος, αντίστοιχα. Για παράδειγμα, το άθροισμα της ακολουθίας

1 , 2 , 3 , 4 _Το n _είναι 1 _{+ a} 2 _{+ a} 3 _{+ … + a} n _{χρησιμοποιώντας την αθροιστική σημείωση ως Σ} n ^{i = 1} _a i _{. i ονομάζεται δείκτης αθροίσματος.}

Χρησιμοποιούνται πολλές παραλλαγές για την άθροιση με βάση την εφαρμογή. Σε ορισμένες περιπτώσεις, το άνω και κάτω όριο μπορεί να δοθεί ως ένα διάστημα ή ένα εύρος, όπως Σ

1≤i≤100 _a i _{και Σ} i∈ [1, 100] _α i _{. Ή μπορεί να δοθεί ως σύνολο αριθμών όπως Σ} i∈P _a i _{, όπου P είναι ένα καθορισμένο σύνολο.}

Σε ορισμένες περιπτώσεις, μπορούν να χρησιμοποιηθούν δύο ή περισσότερα σημάδια σίγμα, αλλά μπορούν να γενικευθούν ως εξής: Σ

j _Σ k _α jk _{= Σ} j _a jk .

Επίσης, το άθροισμα ακολουθεί πολλούς αλγεβρικούς κανόνες. Δεδομένου ότι η ενσωματωμένη λειτουργία είναι η προσθήκη, πολλοί από τους κοινούς κανόνες της άλγεβρας μπορούν να εφαρμοστούν στα ίδια τα ποσά και για τους ξεχωριστούς όρους που απεικονίζονται από την άθροιση.

Περισσότερα για την ενοποίηση

Η ολοκλήρωση ορίζεται ως η αντίστροφη διαδικασία διαφοροποίησης. Αλλά στη γεωμετρική του όψη μπορεί επίσης να θεωρηθεί ως η περιοχή που περικλείεται από την καμπύλη της λειτουργίας και τον άξονα. Επομένως, ο υπολογισμός της περιοχής δίνει την τιμή ενός ορισμένου ολοκλήρου όπως φαίνεται στο διάγραμμα.

Πηγή εικόνας: // en. wikipedia. org / wiki / Αρχείο: Riemann_sum_convergence. png

Η τιμή του οριστικού ολοκλήρου είναι στην πραγματικότητα το άθροισμα των μικρών λωρίδων μέσα στην καμπύλη και στον άξονα.Η περιοχή κάθε λωρίδας είναι το ύψος × πλάτος στο σημείο του εξεταζόμενου άξονα. Το πλάτος είναι μια τιμή που μπορούμε να επιλέξουμε, ας πούμε Δx. Και το ύψος είναι περίπου η τιμή της συνάρτησης στο θεωρημένο σημείο, ας πούμε

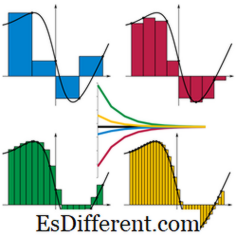
f (x i _{). Από το διάγραμμα, είναι προφανές ότι όσο μικρότερες οι ταινίες είναι καλλίτερες οι ταινίες να ταιριάζουν μέσα στην οριοθετημένη περιοχή, επομένως καλύτερη προσέγγιση της τιμής.} Έτσι, γενικά το καθορισμένο ολοκλήρωμα

I, μεταξύ των σημείων a και b (i. E στο διάστημα [a, b] όπου I f (x 2 n _{) Δx όπου n είναι ο αριθμός των λωρίδων (n = (ba) / Δx).Αυτή η αθροιστική τιμή της περιοχής μπορεί εύκολα να αναπαριστάται με τη χρήση της περιγραφής άθροισμα ως} I n i = 1 _f (x i) Δx. (999)> = lim ^{Δx → 0} _Σ n i = 1 _f i) Δx. Ως γενίκευση από την παραπάνω έννοια, μπορούμε να επιλέξουμε το Δx με βάση το θεωρούμενο διάστημα που είναι ευρετηριασμένο από το i (επιλέγοντας το πλάτος της περιοχής με βάση τη θέση) Ι _{= lim} Δx> 0 ^{Σ n} _{> i} = α _∫ b

f

(x) dx λειτουργία _f (x) στο διάστημα [a, b]. Στην περίπτωση αυτή τα a και b είναι γνωστά ως το ανώτερο και κατώτερο όριο του ολοκληρώματος. Το ενσωματωμένο Reimann αποτελεί βασική μορφή όλων των μεθόδων ενσωμάτωσης. ^{Στην ουσία, η ολοκλήρωση είναι η άθροιση της περιοχής όταν το πλάτος του ορθογωνίου είναι απειροελάχιστο.} _{Ποια είναι η διαφορά μεταξύ ολοκλήρωσης και αθροίσματος;} • Summation είναι η προσθήκη μιας ακολουθίας αριθμών. Συνήθως, η άθροιση δίνεται σε αυτή τη μορφή Σ n _{i = 1 i} όταν οι όροι στην ακολουθία έχουν ένα πρότυπο και μπορούν να εκφραστούν με έναν γενικό όρο. _{• Η ολοκλήρωση είναι βασικά η περιοχή που οριοθετείται από την καμπύλη της λειτουργίας, τον άξονα και τα ανώτερα και κατώτερα όρια. Αυτή η περιοχή μπορεί να δοθεί ως το άθροισμα πολύ μικρότερων περιοχών που περιλαμβάνονται στην οριοθετημένη περιοχή.} • Η άθροιση περιλαμβάνει τις διακριτές τιμές με τα άνω και κάτω όρια, ενώ η ολοκλήρωση περιλαμβάνει συνεχείς τιμές. ^{• Η ενσωμάτωση μπορεί να ερμηνευτεί ως μια ειδική μορφή αθροίσματος.} • Στις μεθόδους αριθμητικών υπολογισμών, η ολοκλήρωση πραγματοποιείται πάντα ως άθροιση.